Excel > Les fonctions liées aux probabilités
Muni de nombreuses et puissantes fonctions numériques, il n’est pas étonnant que ce Tableur (ainsi que ses concurrents) puisse faciliter le travail sur les différents aspects liés aux probabilités.
Les outils liés aux calculs des probabilités :
Factorielle
5! = 4 x 4 x 3 x 2 x 1 = 120. La fonction Excel correspondante est FACT:
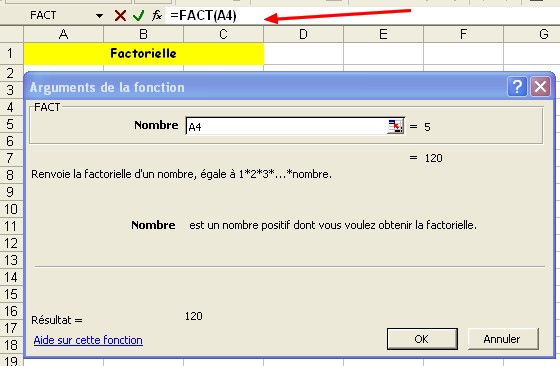
Arrangements
Attention ! Excel parle de permutations, mais fait bien allusion à l’outil Arrangements.
On saisit =PERMUTATION(5 ;3) et on obtient bien 20 qui correspond au nombre d’arrangements de 3 éléments pris parmi 5.(l’ordre intervient ici). On a les formules suivantes:
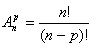ce qui donne 
Avec l’assistant fonctions :
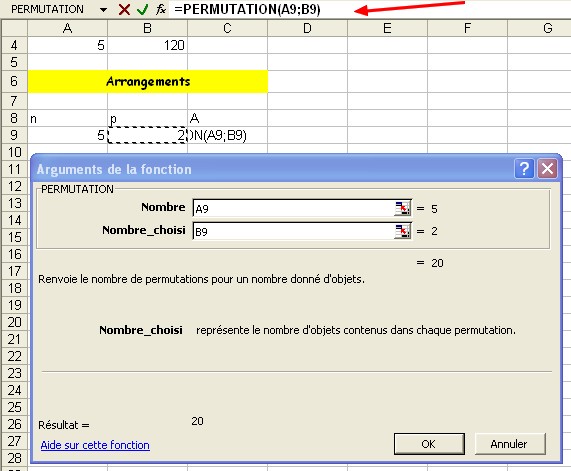
Combinaisons
Pas de gros problèmes là non plus : il suffit de saisir =COMBIN(5;3) pour obtenir le nombre de combinaisons de 3 éléments parmi 5, soit 10 combinaisons.(l’ordre n’intervient pas ici). On a alors:
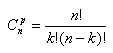soit 
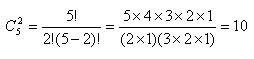
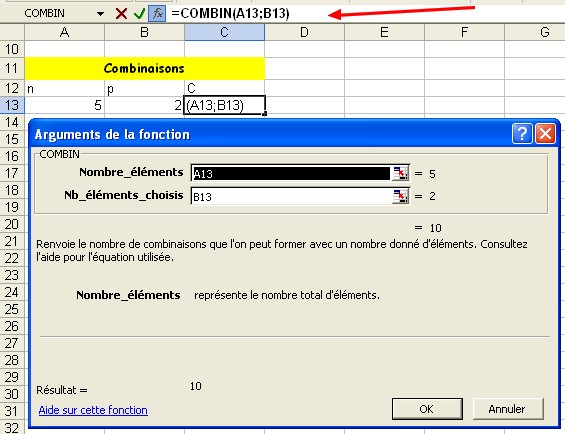
L’assistant fonctions permet d’obtenir la boîte de dialogue suivante, une fois la fonction repérée dans la liste de toutes les fonctions (ou des fonctions statistiques).
Les lois de probabilités
Ces fonctions ont un nom qui débutent toujours par le mot LOI, ce qui permet de les repérer assez facilement. Attention toutefois les fonctions liées aux lois de probabilités sont très nombreuses dans Excel.
Loi binomiale
Celle-ci s'intéresse au nombre de succès (k) (et d'échecs donc) parmi des essais (n) sachant que les probabilités de succès (p) et d'échecs (q=1-p) sont connues. C'est une loi discrète.
Calculons la probabilité d'avoir 3 succès parmi 6 tirages avec une probabilité de succès de 20%:
ce
qui donne ici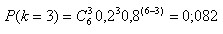 
Quelle est la probabilité d'avoir 8 fois pile en lançant 10 fois une pièce:
Loi de Poisson
Loi dite aussi des phénomènes rares, elle a donc une
variance égale à son espérance mathématique
(
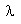). C'est aussi une loi discrète.
Un évènement se produit 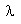fois
en moyenne sur une période. X est la variable aléatoire
représentant le nombre de fois où
l'évènement se produit. X ne peut donc prendre que
des valeurs entières, et suit une loi de
probabilité de Poisson telle que:
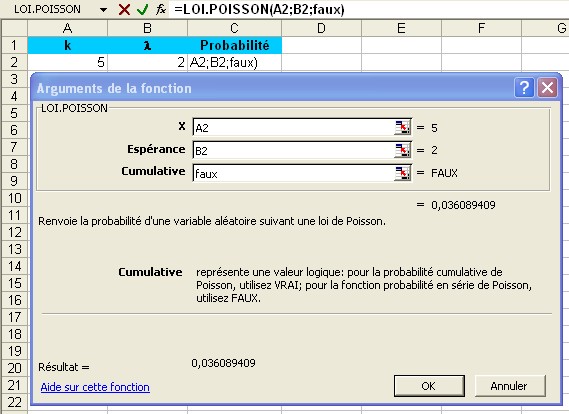
. Si on admet que la moyenne de cet évènement est 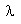= 2 , quelle est la probabilité de voir cet évènement se produire 5 fois? 
soit:
La loi normale
Plusieurs fonctions traitent de cette loi incontournable.
LOI.NORMALE.STANDARD
Cette fonction permet d’obtenir la probabilité cumulée d’une valeur pour la loi normale centrée réduite (Moyenne nulle et écart typeégal à 1). Il s’agit d’une probabilité cumulée, comme pour la lecture dans la table N(0,1).(logique puisque les probabilités ponctuelles sont sans intérêt pour les lois continues) On lit donc bien la probabilité pour que la Variable Aléatoire T (qui suit N(0,1) soit inférieure à la valeur saisie (1 dans la capture d’écran ci-dessous.) La table donne donc: P(T<u), avec T qui suit N(0,1), et u>=0.
Donc:
Pour les intervalles aucun problème puisque cette fonction est utilisable pour des valeurs négatives:
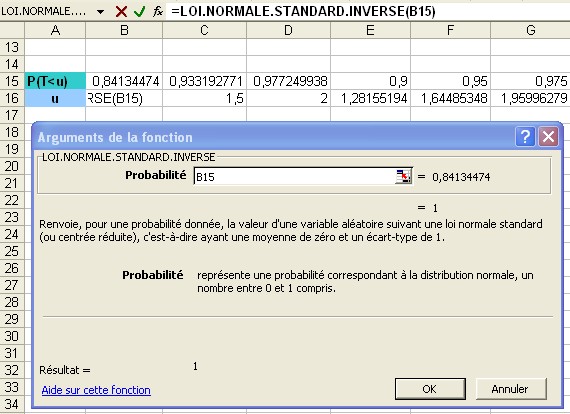
LOI.NORMALE.STANDARD.INVERSE
Celle-ci permet de retrouver la valeur de u à partir d'une probabilité. C'est l'utilisation inverse de la table.
LOI.NORMALE
Même principe mais pour une loi normale quelconque dont on doit donc définir les paramètres (Moyenne et écart type). En prenant pour valeur 0 et 1 on retrouve les résultats précédents pour des valeurs identiques de u. (La plupart du temps les seules probabilités qui nous intéressent dans les lois continues, dont la loi normale, sont les probabilités cumulatives, associées à des intervalles. Contrairement aux loi précédentes (discrètes) les probabilités ponctuelles sont peu utilisées. Aussi on choisra systématiquement VRAI pour l'item Cumulative.):
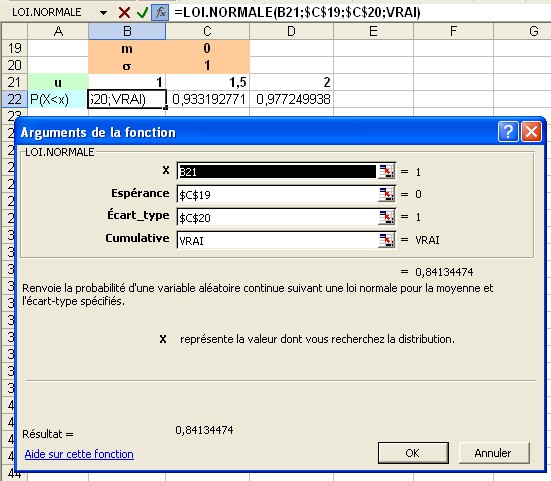
Avec d'autres valeurs on a (pour 15 et 5)
LOI.NORMALE.STANDARD
On retrouve une valeur à partir d'une probabilité:
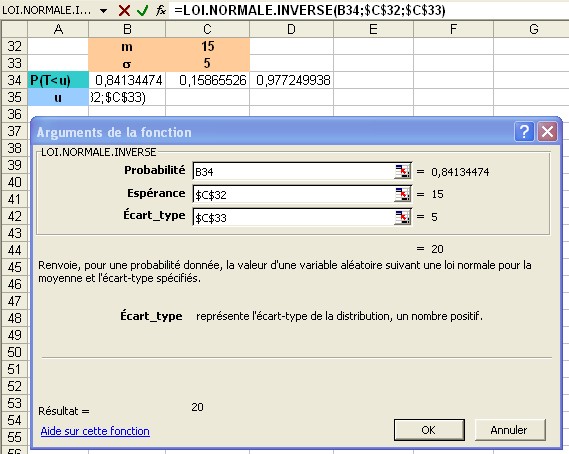
D'où:
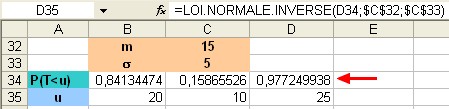
Consulter le fichier Excel correspondant.
